Máximos, mínimos y puntos de inflexión

I.Como localizar puntos máximos y mínimos:

la primer derivada igualándola a cero la cordenada Y se encuentra resolviendo la función de X del vértice f´(x) = 0

Conceptos

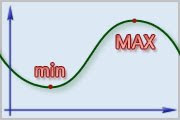
1) Punto máximo local Punto de una gráfica en donde el valor de una función es mayor que el de los puntos circundantes.

2) Punto mínimo local Punto en una gráfica en donde el valor de una función es menor al de todos los puntos circundantes.

3) Punto de inflexión Punto en la gráfica en la cual la pendiente de la tangente cambia su signo. Un punto de inflexión es un punto máximo local o un punto mínimo local.

4) Función cóncava hacia arriba Una función convexa f definida en un intervalo abierto C es continua en C y diferenciable en todos los puntos numerables. Si C es cerrado, f puede no ser continuo en los puntos críticos o finales de C.

5) Función cóncava hacia abajo una función cóncava es lo opuesto de una funcion convexa

Pendiente de una Recta

I. Concepto de pendiente de una recta “m” Imagen 6 (Ingresar la imagen similar a 1.11 de la pendiente de una recta )

es el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta.

II. Fórmula

M= delta Y / delta X

III. Resolver Ejemplo:

Hallar la pendiente de una recta que pasa porS(6,-4), T(2,-3)

M = Yb-Ya/Xb-Xa = 3+4/2-6 = -1.75

la pendiente es 1.75

Distancia entre dos puntos

1. Descripción de distancia entre 2 puntos (pág7) Imagen 4 (Ingresar la imagen de distancia entre 2 puntos)

la distancia entre dos puntos es la longitud del camino más corto entre ambos. es decir, la medición del grado de cercanía que existe entre los dos

II. Fórmula de distancia entre 2 puntos

A(-2,6) y B (1,10)

III. Resolver Ejemplo:

Hallar las coordenadas del punto situado sobre el ejeY equidistante de los puntos M (5,5) y N (4,2).

como el punto pedido P esta sovre el eje Y, y su abscisa es cero, su ordenada la designamos por Y, entonces P (0,y)

la distancia de P a M es
la raiz 2 de (5-0) al cuadrado + (5,y) 2

y la de P a N es
la raiz 2 de (4-o) 2 + (2-y) 2

como ambas deven ser iguales:
la raiz 2 de (5)2 + (5-y)2 es igual que la raiz cuadrada de (4)2 + (2-y) 2

elevamos al cuadrado ambos miembros de la igualdad y efectuamos los cuadrados indicados quedando

25+25-10y+(y)2 = 16+ 4 - 4y + (y)2

candelando (y)2 y dejando en el primer miembro solamente los terminos en y

-10+4y=16+4-25-25

los que nos lleva a Y=5

la respuesta es (0,5)

Ecuaciones Exponenciales

Las ecuaciones exponenciales son aquellas que tienen la incógnita en el exponente

Ejemplo # 1
Para resolver este ejercicio se deben igualar las bases y luego eliminarlas

Ejemplo # 2
Hay que recordar que 1 es igual a cualquier número elevado al exponente cero

Ejemplo # 3
Cuando las bases no son iguales se debe aplicar logaritmo decimal o natural a ambos lados de la igualdad

La función logarítmica

Sea a un número real positivo. La aplicación que a cada número real x>0 le asigna loga x (que es único) se denomina función logarítmica en base a.



Las propiedades de está función se deducen inmediatamente de las de la función exponencial:


a) loga (xy)=loga x+logay para cualesquiera x,yÎ IR.

b) si a es mayor a 1 la función logaritmo correspondiente es estrictamente creciente

c)Para base a mayor a 1 la función logarítmica no esta acotada superior ni inferiormente. De hecho se tiene

d) La función logarítmica es sobreyectiva, es decir para cualquier número real y0 existe un único x0 > 0 tal que loga x0=y0.

e) Para todo número real x>0 se tiene loga x=logbx loga b, cualesquiera que sean los números reales positivos a y b

La función exponencial

Sea a un número real positivo. La aplicación que a cada número real x le asigna la potencia ax se denomina función exponencial de base a.

Las figuras siguientes muestran funciones exponenciales en las que se observan las propiedades que se detallan a continuación.

Propiedades:

a) ax >0 para todo xÎ IR .

b) La función exponencial de base a>1 es estrictamente creciente, mientras que la de base a<1>

c) La función exponencial de base mayor que 1 no está acotada superiormente aunque silo está inferiormente IR. Se tiene

Función racional

Una función racional es una función que se obtiene como cociente de dos funciones polinómicas:

Una función racional está definida en todo IR excepto en los puntos donde el denominador se anula. En su dominio de definición, las funciones racionales son continuas e indefinidamente derivables.